I recently uploaded the implementation of the forward pass of a memory efficient attention algorithm (FlashAttention-2 (Dao et al., 2023)) using Vulkan compute and VK_KHR_cooperative_matrix extension to use Tensor Cores or equivalent hardware to accelerate matrix-matrix multiplications . In this post I will go into the details.

Background

The goal of this project is to provide an open-source, cross-GPU yet efficient implementation of the Scaled Dot Product Attention (SDPA) using open standards (in our case Vulkan + GLSL) to enable as many devices as possible to run Large Language Models (LLMs). As the attention op is one of the main building blocks of LLMs, it is crucial to implement it efficiently in terms of compute and memory.

Currently, multi-head SDPA can be computed by calling PyTorch’s torch.nn.functional.scaled_dot_product_attention function, that accepts the query, key, and value tensors along with the main attention parameters such as scale, dropout and causal masking and returns the attention output. The input matrices contain all attention heads for a single batch of LLM input sequences: the embedding dimension of the model $d_{model}$ is split to $n_{heads}$ parts, resulting an embedding dimension of a single head $d=d_{model}/n_{heads}$, and each attention head can be processed parallel. Therefore all input tensors has 4 dimensions: $b$, $h$, $s$, $d$, where $h$ is the number of heads, and $s$ is the sequence length ($b$ is the number of elements in the batch). In the next section, we focus on the efficient computation of the attention output for a single head.

Memory efficient attention

Note: this is a very brief summary of the FlashAttention-2 paper (Dao, 2023). Recall that attention for a single head is the following computation:

$ \mathbf{S=QK^T} $

$ \mathbf{P}=\text{rowsoftmax}(\mathbf{S})$

$\mathbf{O=PV}$.

Matrices $Q$, $K$, and $V$ are the input matrices and their dimensions are $s \times d$, where $s$ is the context-length of the model that can be tens of thousands, while $d$ (the embedding dimension of a single attention head) is usually 64 or 128.

In order to compute $\text{softmax}$ for a vector $\mathbf{v}$, we need to normalize with the maximum element $v_{max}$ to prevent numerical errors:

$\text{softmax}(\mathbf{v})_i=\frac{e^{v_i-v_{max}}}{\sum_j e^{v_j-v_{max}}}$.

The problem here that in this case we need $s^2$ memory for storing the score matrix $S$ that is too much.

However, the normalized softmax can be computed online, with $\mathcal{O}(1)$ memory using the online softmax trick: we remember only the maximum of the previous elements, and scale the already computed softmax if we found a new maximum as if it was normalized with the newly found maximum value (Rabe et al., 2021).

The FlashAttention-2 algorithm uses the online softmax technique, paired with block- matrix computation: it splits all matrices into blocks, then blocks in a single block row of $\mathbf{S}$, are processed sequentially, while the computation of different block rows of $\mathbf{S}$ can always be computed in parallel. When processing a single block row of $\mathbf{S}$, the maximum is computed blockwise and it is continuously updated while progressing with the blocks horizontally: if the maximum element in the actual block is larger than the maximum element found so far, then we scale the already computed softmax scores to become normalized with the newly found maximum value in the actual block. When the last block is processed in the block row, then all the softmax scores become normalized with the block row-wise maximum as if we had done naive softmax. The number of rows in a block of $\mathbf{S}$ (and $\mathbf{Q}$) is $Br$, while the number of columns in a block of $\mathbf{S}$ (and $\mathbf{K^T}$) is $Bc$. Since we only need to store a small block of S, this algorithm can process very large sequences.

Instead of digesting the equations in the FlashAttention paper, I provide the implementation of the forward pass in the following in Python+Numpy snippet:

def flash_attention_2(Q, K, V, Br, Bc, tau=1.0):
    N = Q.shape[0]
    d = Q.shape[1]
    
    O = np.zeros_like(Q)
    Tr = N // Br
    Tc = N // Bc
    
    for i in range(Tr):
        Qi = block2d(Q, Br, i, d, 0)

        Oi_j = np.zeros((Br, d), O.dtype)
        mi_j = np.full((Br, 1), -np.inf, O.dtype)
        li_j = np.zeros((Br, 1), O.dtype)
        for j in range(Tc):
            Kj = block2d(K, Bc, j, d, 0)
            Vj = block2d(V, Bc, j, d, 0)

            mi_jm1 = np.copy(mi_j)
            li_jm1 = np.copy(li_j)
            Oi_jm1 = np.copy(Oi_j)
            
            Si_j = tau * (Qi @ np.transpose(Kj, (1, 0)))
            mi_j = np.max(
                np.concatenate(
                    [mi_jm1, np.max(Si_j, axis=1, keepdims=True)], axis=1), axis=1, keepdims=True)
            Pijt = np.exp(Si_j - mi_j)
            li_j = np.exp(mi_jm1 - mi_j) * li_jm1 + np.sum(Pijt, axis=1, keepdims=True)
            Oi_j = np.diag(np.squeeze(np.exp(mi_jm1 - mi_j))) @ Oi_jm1 + Pijt @ Vj

        Oi = np.linalg.inv(np.diag(np.squeeze(li_j))) @ Oi_j
        block2d(O, Br, i, d, 0, Oi)
    
    return O

You can tweak the code online using Online Python. See Figure 1 below for the visualization of the blocks.

We have an outer loop, that loops through the block rows, and we have an inner loop that loops through the blocks in the rows. The outer loop can run in parallel, but we need to process the blocks in the inner loop sequentially, because the update for Oi_j in the actual iteration depends on Oi_j computed in the previous iteration according to the online bock softmax.

Vulkan + GLSL implementation

As we saw above, the FlashAttention-2 algorithm can be greatly parallelized: on 3 levels:

• row blocks of a single head can be computed parallel,
• attention heads of a single input can be computed parallel,
• each input of a single batch can be computed parallel.

Thus, the minimum unit that should be computed by the algorithm sequentially is the attention for a single block row.

GPU architecture

We would like to implement FlashAttention-2 on GPU, so we first discuss the programming model briefly.

Computing model

The GPU implements the Single Instruction Multiple Thread (SIMT) computing model. The problem is defined on a grid of threads. Threads run parallel and computes a portion of the input. Threads grouped into blocks and they can cooperate: threads in the same block can communicate using the shared memory and other synchronization primitives. Blocks are split to warps. Threads in the same warp can also communicate directly using synchronization primitives and other collectives. In Vulkan terminology, threads are called invocations, blocks are called workgroups and warps are called subgroups.

GPU implementation details: warp is the minimum unit that can be scheduled to execute on one of the processing units called streaming multiprocessors (SMs) of the GPU consisting of many CUDA cores responsible for executing the threads. On NVIDIA GPUs, the warp size is usually 32, and a warp contains consecutive thread ids and and the first thread is in the first warp. NVIDIA GPUs have 50 to 100+ SMs depending on the actual microarchitecture and GPU model. All warps of a single block will be scheduled to the same SM. NVIDIA GPUs have usually 4 warp schedulers that means that 4 warps can be selected by the execution engine to run simultaneously on a SM.

Memory hierarchy

GPUs have three important levels of memory with respect to latency (and size): global memory with very high latency (visible for all of threads of the grid), shared on-chip memory with low latency (private to the threads of the block), and the fastest type of memory is the registers of the CUDA cores. For efficient GPU utilization, a common strategy is to load as many data to the shared memory and the registers as possible and do as many (useful) computation as we can on the loaded data. Many algorithms can easily become 100 times slower when memory hierarchy is not considered during the algorithm design because the warps cannot be scheduled to actually run the SMs because they are waiting for memory transactions to finish most of the time.

Algorithm

From now, we can focus on the GPU implementation for a single attention head.

The GPU implementation of the algorithm is not so complicated. As the outer loop can be unrolled, we schedule each iteration to a different SM, and the inner loop will be computed with the same SM sequentially in a traditional loop.

Our algorithm can be split into 3 logical parts

• the first part computes the first matrix-matrix multiplication $\mathbf{S}=\mathbf{Q}\mathbf{K^T}$,
• the second part rescales the result by computing the running maximum and sums, while
• the third part computes the second matrix-matrix multiplication: $\mathbf{O}=\mathbf{P}\mathbf{V}$.

Problem tiling

We apply the usual block/warp/subproblem level tiling for the first and last part, as it is the recommended way to efficiently utilize the GPU at least for implementing the GEMM (GEneral Matrix Multiply) operations. See the details on the CUTLASS GEMM API readme or this blogpost from NVIDIA.

Figure 1 shows the blocktiling pattern of each input matrix, while processing the first blocktile of $\mathbf{Q}$ and the second blocktile of $\mathbf{K^T}$. I highlighted the block load/store operations in the Python code snippet: a single block of $\mathbf{Q}$ is loaded once per row, while a block of $\mathbf{V}$ and $\mathbf{K^T}$ is loaded once in every iteration in the sequential inner loop, while $\mathbf{O}$ is written once for every row. Block sizes $Br$ and $Bc$ are tuned to use all the available shared memory.

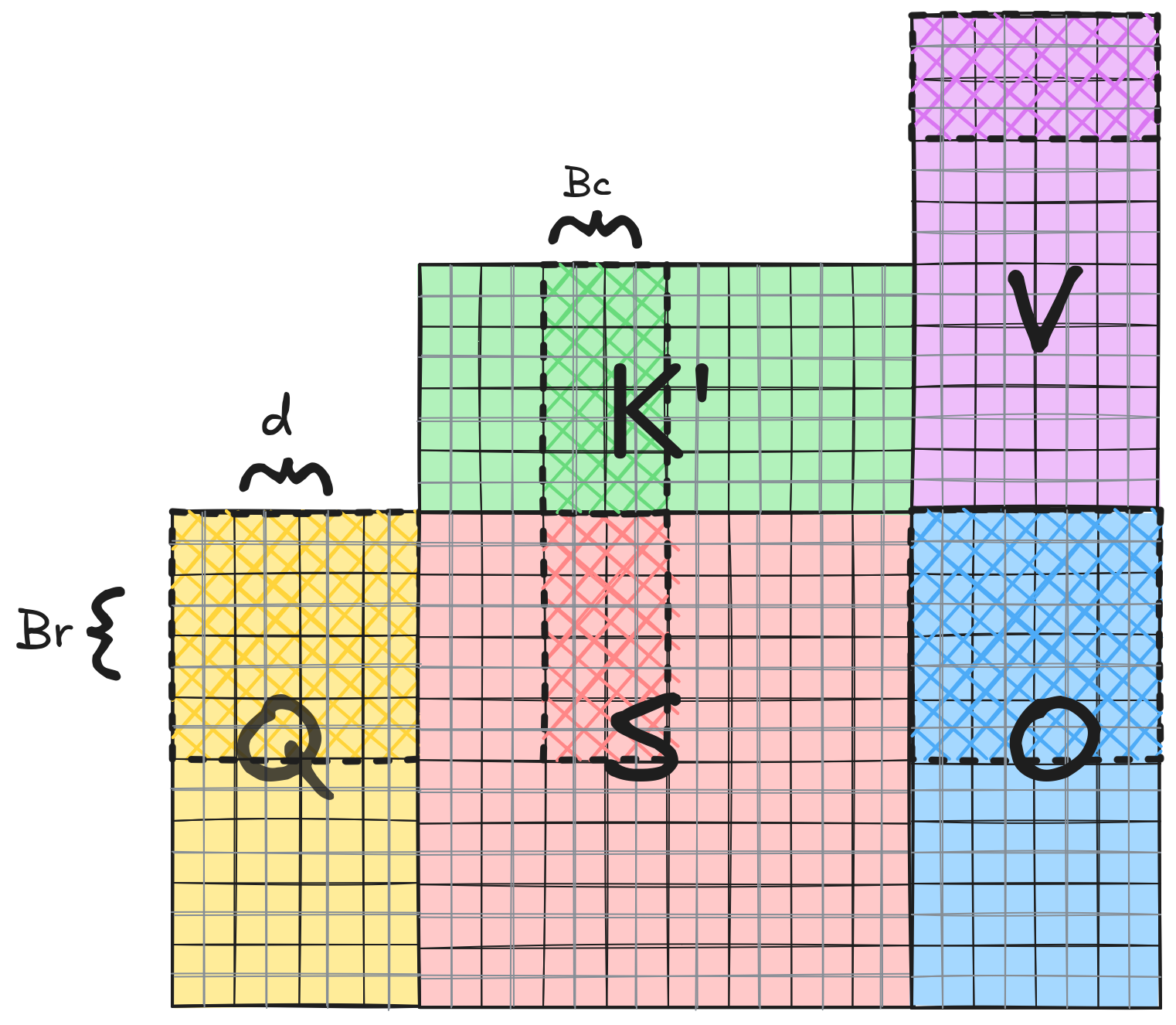
Most NVIDIA GPUs have 4 warp-schedulers so they can physically execute 4 warps at the same time, so we further split the work scheduled to one SM to 4 parts that will run parallel. Figure 2 shows the computation done by the second warp: if we have 8*8 cooperative matrix tiles in the blocktile, then the second warp loads the tiles in row 3 and 4 of blocktile $\mathbf{Q}$, and the whole blocktile of $\mathbf{K^T}$.

To compute the result for a single warp, we need to multiply each cooperative matrix tile. The NVIDIA Volta microarchitecture introduced specialized units to accelerate the computation of small matrix-matrix products called Tensor Cores. The idea is that threads of a single warp cooperate to load fixed-size tiles of matrix multiply operands to the cooperating threads’ registers and then cooperate on warp-level to compute the result. In Vulkan, this is achieved by enabling the VK_KHR_cooperative_matrix extension and calling the API functions in the GLSL shader code.

For example, on my RTX 2060 GPU, the following floating point type cooperative matrix multiply configurations are supported:

Size (MNK): 16x16x16 Types: (AxB+C=D) float16_t x float16_t + float16_t = float16_t
Size (MNK): 16x8x16 Types: (AxB+C=D) float16_t x float16_t + float16_t = float16_t
Size (MNK): 16x8x8 Types: (AxB+C=D) float16_t x float16_t + float16_t = float16_t
Size (MNK): 16x16x16 Types: (AxB+C=D) float16_t x float16_t + float32_t = float32_t
Size (MNK): 16x8x16 Types: (AxB+C=D) float16_t x float16_t + float32_t = float32_t
Size (MNK): 16x8x8 Types: (AxB+C=D) float16_t x float16_t + float32_t = float32_t

Parameter tuning

• The cooperative matrix tile sizes are lM by lK and lK by lN that can be chosen from the supported configurations.
• Warptile size ($\mathbf{Q}$ edge size, $\mathbf{Kt}$ edge size): Wr = Vr * lM and Wc = Vc * lN: the number of coopmats for tiling a warptile.
• Blocktile size ($\mathbf{Q}$ edge size, $\mathbf{Kt}$ edge size): Br = Ur * Wr and Bc = Uc * Wc: Uc is always 1, otherwise we must use atomics.

We wish to load as many data as possible to the shared memory and do as much computation as possible. The main limitation in this case is the shared memory size. According to the CUDA C++ programming guide, the static shared memory size is 48 KB for all devices, and above that we need to use dynamic allocation. Unfortunately, Vulkan does not support dynamic shared memory, so we can only use 48 KB to load the input matrices. Furthermore, we need to add some padding to the matrices as well to prevent shared memory bank conflicts caused by the coopMatLoad instruction when loading the matrix row-by-row in my experience.

A simple strategy that leads the best performance is to use at least 4 warptiles (to run as many warps parallel as possible), then maximize the warptile width, then the warptile height. The warptile width should be maximized to balance the size of the $\mathbf{Q}$ and $\mathbf{K^T}$ blocktiles.

Implementation

To compute the first matrix-matrix multiplication, we initialize an array of Vr*Vc (number of cooperative matrix tiles in a warptile column of $\mathbf{Q}$ multiplied by the number of matrix tiles in a warptile row of $\mathbf{K^T}$, see Figure 2) cooperative matrices to zero (coopMatTilesS) where we will store the final result. Then, we iterate through the inner product dimension ($d$), and load Vc cooperative matrices from from the $\mathbf{K}$ blocktile, then load Vr cooperative matrices from the $\mathbf{Q}$ blocktile. In each iteration, we accumulate the outer product using coopMatMulAdd to get the final result of an $\mathbf{S}$ blocktile. Then, we save the computed tile to the shared memory. Note that this code is executed per warptile.

// Allocate the cooperative matrix tiles for the S warptile.
coopmat<float, gl_ScopeSubgroup, lM, lN, gl_MatrixUseAccumulator> coopMatTilesS[Vr][Vc];

// Initialize the cooopmat tiles.
coopmat<float, gl_ScopeSubgroup, lM, lN, gl_MatrixUseAccumulator> coopMatTilesS[Vr][Vc];
for (int i = 0; i < Vr; i ++) {
    for (int j = 0; j < Vc; j ++) {
        coopMatTilesS[i][j] = coopmat<float, gl_ScopeSubgroup, lM, lN, gl_MatrixUseAccumulator> (float(0.0));
    }
}

// Compute the outer products of the cooperative matrices of the Q and K' warptile and accumulate the result.
for (uint coopMatI = 0; coopMatI < Vd; coopMatI ++) {
    coopmat < float16_t, gl_ScopeSubgroup, lK, lN, gl_MatrixUseB > matKt[Vc];
    for (uint coopMatC = 0; coopMatC < Vc; coopMatC ++) {
        uvec2 coopMatTileCoordShKt = warpTileCoordShKt + uvec2(coopMatI * lK, coopMatC * lN);
        coopMatLoad(matKt[coopMatC], sharedKt, coordToOffset(coopMatTileCoordShKt, strideSharedKt) / granularitySharedKt, strideSharedKt/granularitySharedKt, gl_CooperativeMatrixLayoutRowMajor);
    }

    coopmat<float16_t, gl_ScopeSubgroup, lM, lK, gl_MatrixUseA> matQ[Vr];
    for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
        uvec2 coopMatTileCoordShQ = warpTileCoordShQ + uvec2(coopMatR * lM, coopMatI * lK);
        coopMatLoad(matQ[coopMatR], sharedQ, coordToOffset(coopMatTileCoordShQ, strideSharedQ) / granularitySharedQ, strideSharedQ / granularitySharedQ, gl_CooperativeMatrixLayoutRowMajor);
    }

    for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
        for (uint coopMatC = 0; coopMatC < Vc; coopMatC ++) {
            coopMatTilesS[coopMatR][coopMatC] = coopMatMulAdd(matQ[coopMatR], matKt[coopMatC], coopMatTilesS[coopMatR][coopMatC]);
        }
    }
}

// Save the copmuted warptile to the shared memory.
for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
    for (uint coopMatC = 0; coopMatC < Vc; coopMatC ++) {
        uvec2 coopMatTileCoordShS = warpTileCoordShS + uvec2(coopMatR * lM, coopMatC * lN);
        coopMatStore(float(scaling) * coopMatTilesS[coopMatR][coopMatC], sharedS, coordToOffset(coopMatTileCoordShS, strideSharedS) / granularitySharedS, strideSharedS / granularitySharedS, gl_CooperativeMatrixLayoutRowMajor);
    }
}

Once all the warptiles of $\mathbf{S}$ are computed, and saved to the shared memory we proceed with the middle part of the algorithm to scale the results. Saving $\mathbf{S}$ to the shared memory is unavoidalbe currently, because the Vulkan API does not allow us to manipulate cooperative matrices in the registers directly: we need to load the results back from the shared memory to the registers at the beginning of the second part, and compute the scaling. After $\mathbf{S}$ is in the registers, each thread processes a different row from the matrix. As 128 threads can run concurrently when GPU resources are fully utilized, we need to set $Br=128$ thus each warptile should process at least Vr=2 cooperative matrices (each has 16 rows) from $\mathbf{Q}$ simultaneously. Once we are ready with the rescaling of the $\mathbf{S}$ blocktile (resulting in $\mathbf{P}$), we save it to the shared memory and jump to the third part to compute the final result ($\mathbf{O}$).

In the third part, we allocate an array of Vr*Vd (number of cooperative matrix tiles in a column of warptile from $\mathbf{S}$ multiplied by the number of cooperative matrix tiles in a row of warptile from $\mathbf{V}$, see Figure 2) cooperative matrices (coopMatTilesO), and initialize it with the blocktile $\mathbf{O}$ that was computed in the previous iteration. Then, we compute the outer products in each iteration and accumulate them before storing the result to the shared after the last inner-product iteration:

// Allocate the cooperative matrix tiles for the O warptile.
coopmat<float, gl_ScopeSubgroup, lM, lK, gl_MatrixUseAccumulator> coopMatTilesO[Vr][Vd];

// Load the scaled O from the shared memory to the coopmat tiles.
[[unroll]] for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
    [[unroll]] for (uint coopMatC = 0; coopMatC < Vd; coopMatC ++) {
        uvec2 coopMatTileCoordShO = warpTileCoordShO + uvec2(coopMatR * lM, coopMatC * lK);
        coopMatLoad(coopMatTilesO[coopMatR][coopMatC], sharedO, coordToOffset(coopMatTileCoordShO, strideSharedO) / granularitySharedO, strideSharedO / granularitySharedO, gl_CooperativeMatrixLayoutRowMajor);
    }
}
// Compute the outer products of the cooperative matrices of the P and V warptile and accumulate the result.
[[unroll]] for (uint coopMatI = 0; coopMatI < Vc; coopMatI ++) {
    coopmat<float16_t, gl_ScopeSubgroup, lM, lN, gl_MatrixUseA> matS[Vr];
    [[unroll]] for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
        uvec2 coopMatTileCoordShS = warpTileCoordShS + uvec2(coopMatR * lM, coopMatI * lN);
        coopMatLoad(matS[coopMatR], sharedS, coordToOffset(coopMatTileCoordShS, strideSharedS) / granularitySharedS, strideSharedS / granularitySharedS, gl_CooperativeMatrixLayoutRowMajor);
    }
    coopmat<float16_t, gl_ScopeSubgroup, lN, lK, gl_MatrixUseB> matV[Vd];
    [[unroll]] for (uint coopMatC = 0; coopMatC < Vd; coopMatC ++) {
        uvec2 coopMatTileCoordShV = warpTileCoordShV + uvec2(coopMatI * lN, coopMatC * lK);
        coopMatLoad(matV[coopMatC], sharedV, coordToOffset(coopMatTileCoordShV, strideSharedV) / granularitySharedV, strideSharedV / granularitySharedV, gl_CooperativeMatrixLayoutRowMajor);
    }

    [[unroll]] for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
        [[unroll]] for (uint coopMatC = 0; coopMatC < Vd; coopMatC ++) {
            coopMatTilesO[coopMatR][coopMatC] = coopMatMulAdd(matS[coopMatR], matV[coopMatC], coopMatTilesO[coopMatR][coopMatC]);
        }
    }
}

// Save the copmuted warptile to the shared memory.
[[unroll]] for (uint coopMatR = 0; coopMatR < Vr; coopMatR ++) {
    [[unroll]] for (uint coopMatC = 0; coopMatC < Vd; coopMatC ++) {
        uvec2 coopMatTileCoordShO = warpTileCoordShO + uvec2(coopMatR * lM, coopMatC * lK);
        coopMatStore(coopMatTilesO[coopMatR][coopMatC], sharedO, coordToOffset(coopMatTileCoordShO, strideSharedO) / granularitySharedO, strideSharedO / granularitySharedO, gl_CooperativeMatrixLayoutRowMajor);
    }
}

Performance

FP16 performance was tested with different sequence lengths and two head dimensions $d$=64 and $d$=128. The batch dimension was 4 and the number of heads was 8.

The peak performance reached by the kernel is 17.1086 TFLOPS when $d$=64 and 10.0235 TFLOPS when $d$=128. The theoretical Tensor TFLOPS performance of my RTX 2060 SUPER GPU is 57.4 TFLOPS, therefore the algorithm can approach 30% of the theoretical maximum. It would be interesting to test what is the improvement compared to when we do not use Tensor Cores at all (half precision theoretical maximum is 12.46 FLOPS — $d$=64 can outperform this). This is not that bad as there are serious limitations when using the GPU through the Vulkan API:

• Cooperative matrices can only be moved between the registers and the shared memory or the global memory. Results, or loaded matrices cannot be modified while they reside in the registers (except that we can use pointwise tensor ops).
• Shared memory limitation: we cannot use dynamic memory allocation, so only 48 KB can be used to load the tiles, while we can use all the available shared memory through CUDA, that can be as much as 2 times more that that of available to Vulkan depending on the GPU generation).

I do not know yet, why the performance drops from 17 TFLOPS to 10 when switching to $d$=128 from 64. The reason could be simply that in the first case, tiles are larger in the $d$-dimension, so we cannot load as large tiles. While we can schedule 4 warptiles with each tile having 4 “coopmat-width” when $d$=64, we can only load 1 coopmat-width warptiles when scheduling 4 parallel warps if $d$=128. Once I will be able to profile my Vulkan kernels, I will further optimize it.

Check the code at: https://github.com/etasnadi/VulkanCooperativeMatrixAttention/.

References

Dao: FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning, 2023.
Rabe et al.: Self-attention does not need $\mathcal{O}(n^2)$ memory, 2021.

Cover image is downloaded from Pexels.